The Fermi Paradox
The story goes that Italian-American physicist Enrico Fermi, who at the time was working on the atomic bomb at Los Alamos National Laboratory, sat with his co workers at lunch discussing various topics. Interrupting everybody he suddenly yelled: "Where is everybody?”. And so the famous Fermi Paradox was born. After a quick back-of-the-envelope calculation he concluded that our universe should be teeming with life! However, we have not yet found any (convincing) evidence! How can both of these seemingly paradoxical statements be true1? In this post I want to discuss what the Fermi Paradox is, why we (or rather humanity as a whole) might care, and some possible resolutions.
The Number of Aliens
To see how the Fermi paradox comes about we want to estimate the number of possible alien civilizations that we could observe in our galaxy. I originally planned on using the Drake Equation in this part, but then I thought it might be both more interesting and informative to come up with my own estimate. I will be doing this by getting the best estimates where I can, and making up numbers elsewhere.
We will try to make very conservative estimations to get a lower bound on the number stars that could have life. We will assume that only earth-like planets with earth-like temperatures around sun-like stars can have life. This will most definitely undercount planets with life, as we know that there is life that is pretty weird just on this planet, but there could be even weirder life!
We should probably start with the number of stars in our galaxy. This is usually estimated around 100-400 billion. Only around 10% of stars are sun-like (i.e. G/K-type). We also know that more than 10 % of sun-like stars have a planet in their habitable zone. Combining all of these (conservative) numbers we are left with 100 billion * 10% * 10% = 1 billion possible star systems with life-supporting planet(s).
Life?
Now comes the difficult question: how many of these planets might have life that we can detect? Let us start off with some numbers. Our Earth is approximately 4.5 billion years old, which is also roughly the age of our sun. Our sun can (only) get around 10 billion years old (though K-type stars can get much older). Life definitely got started 3.7 billions years ago, but might have got going as early as 4.2 billion years ago. In other words, life got started the very second it possibly could! This suggests that under the right conditions, i.e. the ones we assumed, life appears fairly quickly and easily (on these timescales). Drake agrees with us, he estimated that 100% of these planets would have some form of life. This evidence is strengthened even more by the fact that our universe is only 13.8 billions years old, and so stars like our sun are fairly new. An argument against the prevalence of (detectable life) this is that stars like ours will form for at least another 1-100 trillion years, making us seem atypically early. I will come back to this fact in the section on why we are so early.
For now, all we need to know is that I believe the probability of (some) life emerging on an earth-like planet is basically 100%. Intelligent life however is not as clear. We only emerged after roughly half our stars life-span. Accounting for civilizations destroying themselves before being able to properly pollute space with radio signals, or making themselves noticeable in more flashy ways, is pretty difficult and basically guesswork. Just making up a number, I will say that around 1% of habitable planets have life that we might detect.
This leaves us with ~10 million stars from which we might receive a signal. That is a lot. Assuming our galaxy is flat and stars uniformly distributed (a rough but not terrible assumption), we would expect that the closest star with life is only around 100 lightyears away! So where are they? Where are all the aliens?
There are admittedly a lot of issues with the above model. I did not explicitly account for the age of stars, the rate of star birth and the average age of detectable civilizations. Also, if you think the 1% figure for detectable intelligent life I chose is too high, then I implore you to plug in your own guess and see how it affects the outcome!
Proponents of lower estimates say that civilizations only exist for ~6500 years on average before irreversibly destroying themselves, which at a star-generation of ~1 new star a year puts this estimate way below 1%. I believe this to be too pessimistic.
Before we move on I suggest you look at this incredible high res picture of the milky way.
We are really early!
As stated earlier, star formation will most likely continue for around 1-100 trillion years! This means that we are at most 1% into the era in which life could exist. Just to explain how insane that is I made the following chart:
Even if you are not concerned with aliens, this seems very unlikely, and might reveal something to us about our universe. Since, as any good Bayesian will tell you, if you see an unlikely event you might want to consider a hypothesis that makes that event more likely.
I stole this idea from economist, weird-ideas-haver, Robin Hanson, although he is not the first to notice. This lead him to write a paper with physicist Daniel Martin, computer scientist Calvin McCarter and Jonathan Paulson who’s at some trading firm I guess?
This paper is really what I wanted to talk about in this post. If you have managed to make it until here, now comes the juicy part!
Hanson et. al. looked at the fact that we are early and concluded that the assumptions we implicitly made are unlikely and that we should instead favor assumptions that make our earliness seem more likely. They used a more sophisticated model to come to the conclusion that we are early, but the main takeaway is the same.
We implicitly assumed that being created in any time of the universe is equally likely, but that does not need to be true! There might be some future event that renders the spawning of new life unlikely or even impossible. If such a deadline exists, then we would not seem so early. Their model also explains why we do not yet see any aliens, and why seeing alien civilizations might be very troubling.
Grabby Aliens
Their solution is grabby aliens. Grabby aliens are aliens that fulfill the following criteria:
They expand their occupied territory at some positive fraction of the speed of light,
observably change the occupied regions,
are born at some constant rate, but only in uncontrolled territory.
This is contrasted with quiet aliens, which either do not expand or do not observably change the regions they control. We can safely ignore these for now.
So let us jump in to the model they use for grabby aliens. Their model has three parameters. First, the rate at which grabby civilizations are born. We can estimate this parameter by the emergence of humans, since we have some strictly positive probability that we might turn grabby.
Second, the rate of expansion of grabby civilizations. By our assumptions, no new civilizations will be born in the expanded region, and we should be able to see them, as they are observably changed. Note that for a civilization to expand their biology, they do not physically have to visit each star they go to. They will most likely send out robots like von Neumann probes.
The final parameter comes from The Great Filter model, also invented by Hanson. It is the number of so-called hard steps that dead matter needs to take to become a grabby civilization. The more hard steps there are the more difficult it is to become a grabby civilization, that is: hard steps are hard. This together with the rate gives us a power-law for the occurrences of grabby civilizations in a region of space-time (don’t worry if you don’t know what a power-law is).
A model for how grabby aliens will dominate a region of space-time.
The first and third parameters can be estimated by observations of our own species. First, assuming that humans are “usual” amongst all possible grabby civilizations, we can estimate the rate at which grabby civilizations are born. If the rate were higher, it would make us seem very late, and if the rate were lower we would look too early, again. Next, we can estimate the number of hard steps by looking at the history of our evolution and the difficulties we have to still overcome to become grabby. We expect to have at least 6 hard steps.
Examples of hard steps could be the start of some reproductive system (e.g. RNA, DNA). The beginning of single cellular life. Moving from asexual reproduction to sexual reproduction. The creation of general intelligence in a species. There might also still be a hard step ahead of us, which would not be good!
What about the expansion speed for super advanced high tech alien civilizations? How could be possible estimate this parameter?
Back to the Fermi
Here the Fermi paradox comes to our aid. We can use the fact that we have not seen any aliens to estimate expansion speeds. This can be done using a selection effect. Since we have been created, we are by our assumptions not already in an occupied region. We also do not already see aliens in our light cone/in our sky, which by our assumptions we would, if they were there. If we could see grabby aliens in the sky we would expect them to take up a larger proportion than moon currently does.
We expect high expansion speeds, since if aliens expanded more slowly, there would be a larger chance of us being able see them without them already being here. In other words, if expansion speeds were very slow it would increase the likelihood of us having already seen them. This can be seen in the following chart (taken from the paper):
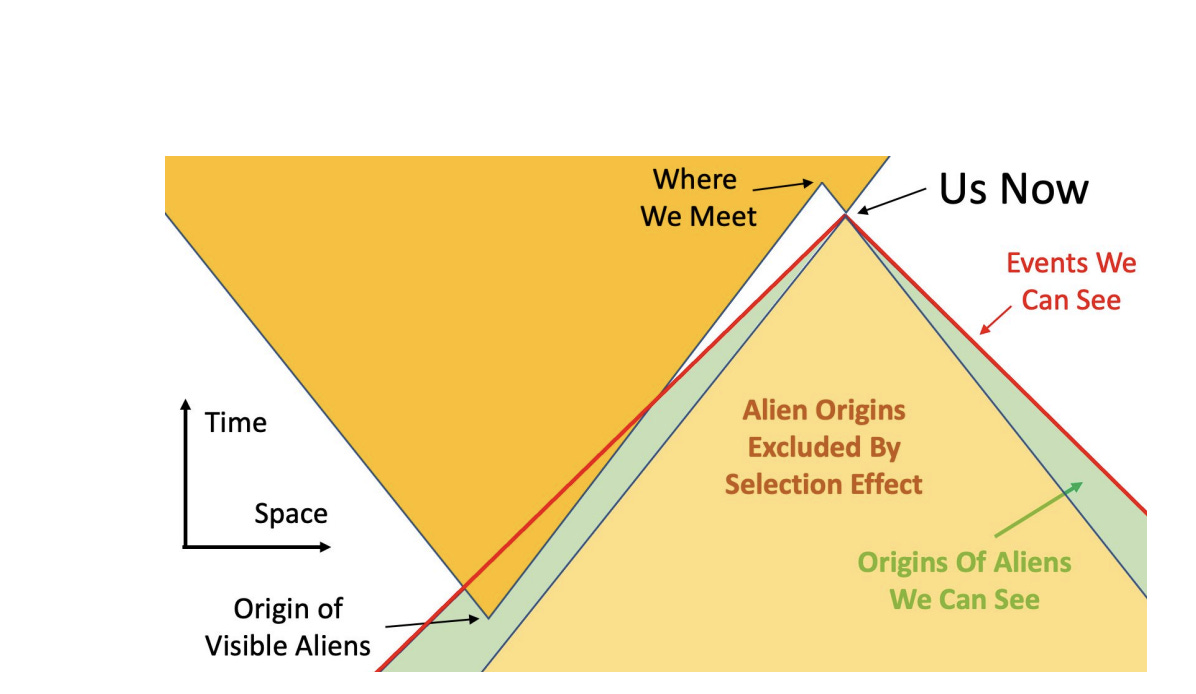
The green area of possible visible aliens grows larger the slower they expand, or, the area of aliens excluded by the selection effect would grow narrower. This model predicts that aliens will expand at least at 25% the speed of light! This could possibly be achieved by things like solar sails. Furthermore, faster expansion speeds make later civilizations less likely, as there is less unoccupied territory for them to be born.
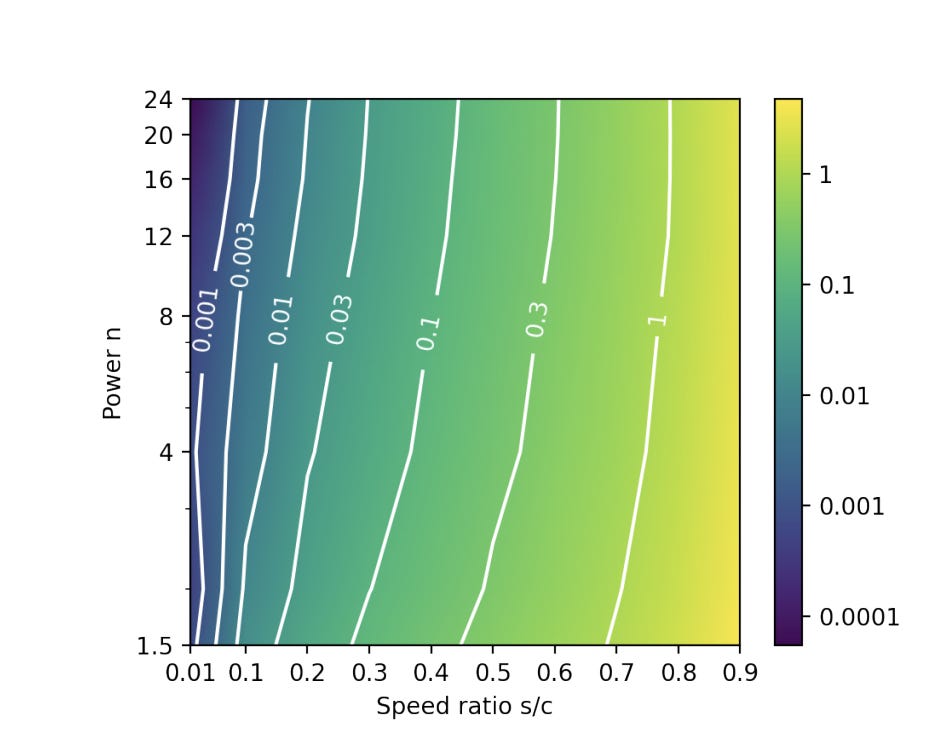
To better understand this you can look at the following graph. The lines describe likelihood ratios of us seeing no aliens. Parameter n is the number of hard steps and speed ratio s/c is the expansion rate. The higher the likelihood ratio, the better it explains the evidence of us seeing no aliens. So assuming the model is correct, faster aliens better explain us not seeing aliens.
What does this mean for us?
Now that we have the model, and can simulate it using the estimated parameters we can see what happens. The first prediction is that most grabby civilizations should occur in the first 50 billion years of our universe, depending on the number n of hard steps. The fact that all of these lines cross at the same point is no coincident, it stems from the fact that we assume humans to be “typical”.
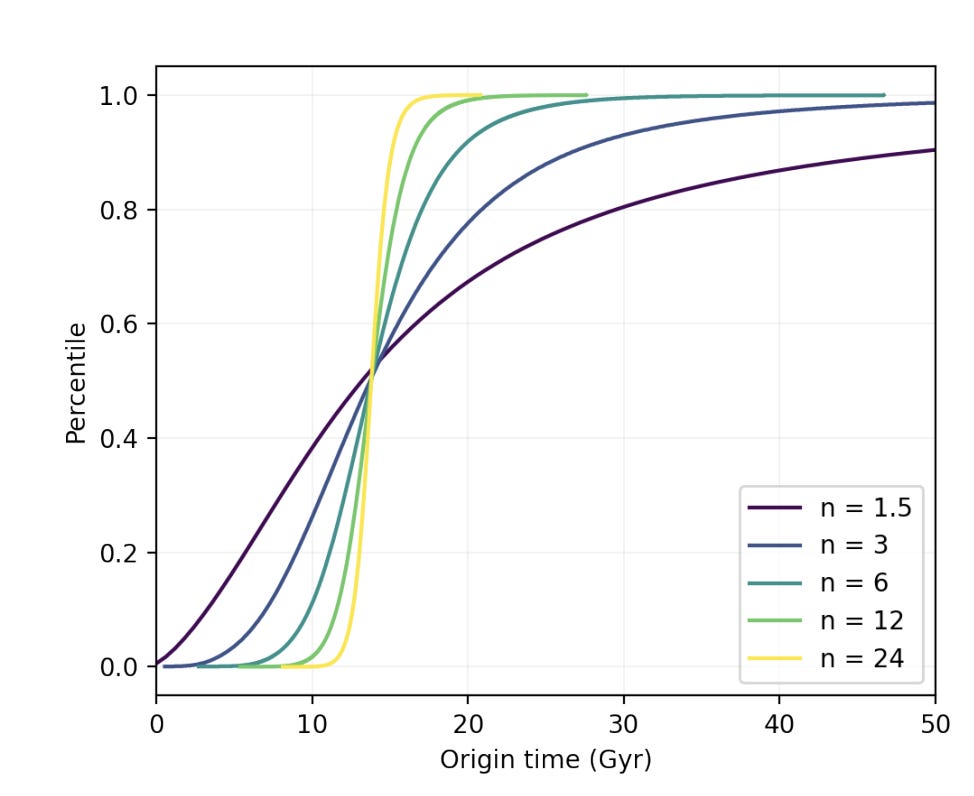
You can see in the above graph that if life becomes less likely (more hard steps) that most civilizations are born in a very short amount of time. This is a natural consequence of the power-law model of civilizational birth.
If we assume a galaxy to be a collection of at least one million stars, the model also predicts the number of galaxies controlled by a typical grabby civilizations before it meets another grabby civilization.
So if we become grabby, we would expect to control 10,000 to 100,000,000 galaxies by the time we meet another civilization.
Finally let us turn to the following two questions, how likely is that we will become grabby, and how likely is it that we will observe other non-grabby civilizations? These two questions turn out to be closely related.
The model assumes that every grabby civilization was once non-grabby, and that each non-grabby civilization has a chance 1/R of becoming grabby. This means that non-grabby civilizations are R times more common than grabby ones.
For our chances to become grabby we would want to have a low R. This would be good for our long term chances of survival, as a high value of R could mean that some other grabby civilization will eventually swallow us.
On the other hand, for us to observe a non-grabby civilization we would want a very high value of R, which makes sense on two fronts, first if R is lower there will be fewer grabby civilizations to observe and second the ones we might observe have a higher chance of getting colonizes by grabby ones. For us to have a decent chance to observe non-grabby aliens we should expect R to be at least 1000.
This means that observing non-grabby civilizations could be very bad news for us, as it would mean that R is more likely to be big! This should make us weary about that fact that maybe we already have.
Conclusion
This article is already fairly long so I will try to keep this part short. I give the grabby aliens model a good chance of being true. To reject this model you would have to come up with an alternative that explains both why we seem so early and why we do not see any aliens yet and is more convincing. The model described in the paper is, by the authors own admission, somewhat simplified - only relying on three parameters. The conclusions it draws should still be mostly true however.
While we might not want to become a [grabby civilization], many of the scenarios in which we do not are because we can not. For example, we may go extinct, or become permanently and strongly limited. So we might at least like to have the option to become grabby.
If you are skeptical of humans abilities however, at least you will be in good company with Monty Python.
Todays paradox is veridical.